笔记主要记录三部分内容。第一部分记录词向量的概念和训练方法，第二部分记录如何用哈夫曼树加速网络的训练，第三部分记录word2vec的功能和实现方法。内容整理于网络。

词向量

词向量是一种低维实数向量。这种向量一般长成这个样子：[0.792, −0.177, −0.107, 0.109, −0.542, ...]。维度以 50 维和 100 维比较常见。

1. 词向量的来历

Distributed representation 最早是 Hinton 在 1986 年的论文《Learning distributed representations of concepts》中提出的。

如果用传统的稀疏表示法表示词，在解决某些任务的时候（比如构建语言模型）会造成维数灾难[Bengio 2003]。使用低维的词向量就没这样的问题。同时从实践上看，高维的特征如果要套用 Deep Learning，其复杂度几乎是难以接受的，因此低维的词向量在这里也饱受追捧。
相似词的词向量距离相近，这就让基于词向量设计的一些模型自带平滑功能，让模型看起来非常的漂亮。

2. 词向量的训练

    要介绍词向量是怎么训练得到的，就不得不提到语言模型。到目前为止我了解到的所有训练方法都是在训练语言模型的同时，顺便得到词向量的。
    这也比较容易理解，要从一段无标注的自然文本中学习出一些东西，无非就是统计出词频、词的共现、词的搭配之类的信息。而要从自然文本中统计并建立一个语言模型，无疑是要求最为精确的一个任务（也不排除以后有人创造出更好更有用的方法）。既然构建语言模型这一任务要求这么高，其中必然也需要对语言进行更精细的统计和分析，同时也会需要更好的模型，更大的数据来支撑。目前最好的词向量都来自于此，也就不难理解了。
    这里介绍的工作均为从大量未标注的普通文本数据中无监督地学习出词向量（语言模型本来就是基于这个想法而来的），可以猜测，如果用上了有标注的语料，训练词向量的方法肯定会更多。不过视目前的语料规模，还是使用未标注语料的方法靠谱一些。

2.0 语言模型简介

    语言模型其实就是看一句话是不是正常人说出来的。比如机器翻译、语音识别得到若干候选之后，可以利用语言模型挑一个尽量靠谱的结果。在 NLP 的其它任务里也都能用到。
    语言模型形式化的描述就是给定一个字符串，看它是自然语言的概率 P(w1,w2,…,wt)。w1 到 wt 依次表示这句话中的各个词。有个很简单的推论是：
P(w1,w2,…,wt)=P(w1)×P(w2|w1)×P(w3|w1,w2)×…×P(wt|w1,w2,…,wt−1)
    常用的语言模型都是在近似地求 P(wt|w1,w2,…,wt−1)。比如 n-gram 模型就是用 P(wt|wt−n+1,…,wt−1) 近似表示前者。

2.1 Bengio 的经典之作

训练语言模型的最经典之作，要数 Bengio 等人在 2001 年发表在 NIPS 上的文章《A Neural Probabilistic Language Model》。当然现在看的话，肯定是要看他在 2003 年投到 JMLR 上的同名论文了。

Bengio 用了一个三层的神经网络来构建语言模型，同样也是 n-gram 模型。如图1。

图1

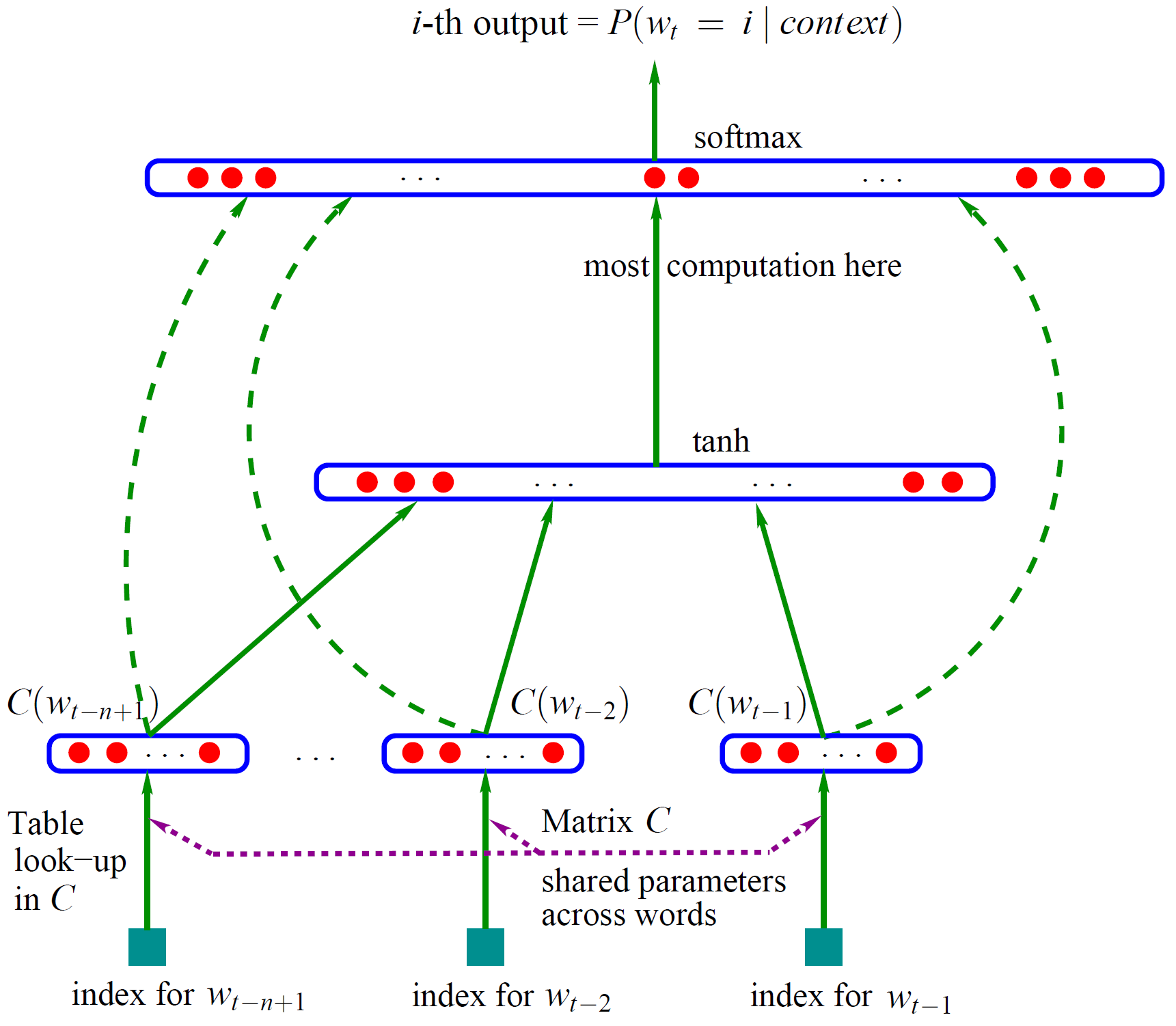
    图中最下方的 wt−n+1,…,wt−2,wt−1 就是前 n−1 个词。现在需要根据这已知的 n−1 个词预测下一个词 wt。C(w) 表示词 w 所对应的词向量，整个模型中使用的是一套唯一的词向量，存在矩阵 C（一个 |V|×m 的矩阵）中。其中 |V| 表示词表的大小（语料中的总词数），m 表示词向量的维度。w 到 C(w) 的转化就是从矩阵中取出一行。
    网络的第一层（输入层）是将 C(wt−n+1),…,C(wt−2),C(wt−1) 这 n−1 个向量首尾相接拼起来，形成一个 (n−1)m 维的向量，下面记为 x。
    网络的第二层（隐藏层）就如同普通的神经网络，直接使用 d+Hx 计算得到。d 是一个偏置项。在此之后，使用 tanh 作为激活函数。
    网络的第三层（输出层）一共有 |V| 个节点，每个节点 yi 表示下一个词为 i 的未归一化 log 概率。最后使用 softmax 激活函数将输出值 y 归一化成概率。最终，y 的计算公式为：

y=b+Wx+Utanh(d+Hx)

式子中的 U（一个 |V|×h 的矩阵）是隐藏层到输出层的参数，整个模型的多数计算集中在 U 和隐藏层的矩阵乘法中。后文的提到的 3 个工作，都有对这一环节的简化，提升计算的速度。
式子中还有一个矩阵 W（|V|×(n−1)m），这个矩阵包含了从输入层到输出层的直连边。直连边就是从输入层直接到输出层的一个线性变换，好像也是神经网络中的一种常用技巧（没有仔细考察过）。如果不需要直连边的话，将 W 置为 0 就可以了。在最后的实验中，Bengio 发现直连边虽然不能提升模型效果，但是可以少一半的迭代次数。同时他也猜想如果没有直连边，可能可以生成更好的词向量。

现在万事俱备，用随机梯度下降法把这个模型优化出来就可以了。需要注意的是，一般神经网络的输入层只是一个输入值，而在这里，输入层 x 也是参数（存在 C 中），也是需要优化的。优化结束之后，词向量有了，语言模型也有了。
这样得到的语言模型自带平滑，无需传统 n-gram 模型中那些复杂的平滑算法。Bengio 在 APNews 数据集上做的对比实验也表明他的模型效果比精心设计平滑算法的普通 n-gram 算法要好 10% 到 20%。

哈夫曼树加速网络训练

    前面已经提过语言模型的目标就是判断一句话是否是正常的，至于怎么判断则需要计算很多条件概率如 p(w_i|content_i)，然后还要把这些条件概率连乘起来得到联合概率。这样就带来了问题了——怎么去计算 p(w_i|content_i) ，这里的word2vec的计算这个条件概率的方法是利用神经网络的能量函数，因为在能量模型中，能量函数的功能是把神经网络的状态转化为概率表示。既然是能量模型，那么就需要能量函数，word2vec定义了一个非常简单的能量函数 E(A,C)=-(A∙C)。其中A可以认为是某个词的词向量，C是这个词的上下文的词向量的和（向量的和），基本上就可以认为C代表Context；中间的点号表示两个向量的内积。
    然后根据能量模型（这个模型假设了温度一直是1，所以能量函数没有分母了），就可以表示出词A的在上下文词向量C下的概率来了
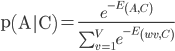
jQVV3m.png!web.png
    其中V表示语料库里面的的词的个数，这个定义的意思是在上下文C出现的情况下，中间这个词是A的概率，为了计算这个概率，肯定得把语料库里面所有的词的能量都算一次，然后再根据词A的能量，那个比值就是出现A的概率。

这个概率其实并不好统计，为了算一个词的的概率，得算上这种上下文的情况下所有词的能量，然后计算指数值再加和，这是最耗时间的部分。这里科学家们采用条件概率和二分的方法，将语料库的规模每次减半，以减少计算量。假如把语料库的所有词分成两类，分别称为G类和H类，每类一半，其中词A属于G类，那么下面的式子就可以成立了 p(A│C)=p(A|G,C)p(G|C)。p(A|G,C)还可以继续二分为两类，知道每类里只有一个词，即到了树的叶子节点。此时p(A|C) 等于树上从根节点到叶子节点的路径概率乘积，跟其他节点没有关系，训练网络时只需要计算这条路径上的节点以及他们的直系兄弟节点误差，并反向传播。如果没有使用这种二叉树，而是直接从隐层直接计算每一个输出的概率——即传统的softmax，就需要对|V|中的每一个词都算一遍，这个过程时间复杂度是 O(|V|)的。而使用了二叉树（如word2vec中的Huffman树），其时间复杂度就降到了O(log2(|V|))。

如前所述，使用不断二分产生的二叉树可以降低训练时的计算量。在一个语料库中，单词出现的频率并不均匀，出现频率高的单词训练时他所在路径上节点被更新的次数就多，如果能让这个路径尽可能的短，那么还可以进一步减少计算量。这刚好是哈夫曼树的效果。

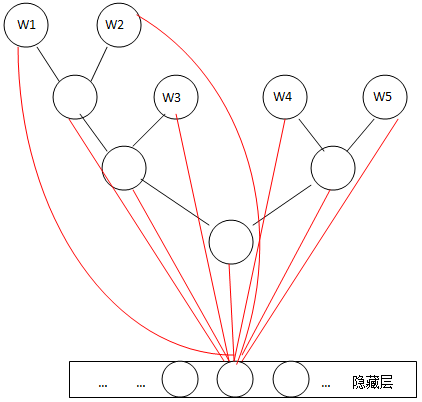
E4IHTL`(~WON1R$W0)1O~GG.png

图2

此时的网络，将最后的输出层改成了哈夫曼树，隐藏层的每一个神经元与树中的每一个节点相连。

在训练阶段，当给定一个上下文，要预测后面的词(Wn)的时候（word2vec的CBOW和Skip-gram都不是预测后面的词，都是在中间的词上做文章，但是本文这么写并不影响理解），实际上我们知道要的是哪个词(Wn)，而Wn是肯定存在于二叉树的叶子节点的，因此它必然有一个二进制编号，如"010011"，那么接下来我们就从二叉树的根节点一个个地去便利，而这里的目标就是预测这个词的二进制编号的每一位！即对于给定的上下文，我们的目标是使得预测词的二进制编码概率最大。形象地说，我们希望在根节点，词向量和与根节点相连经过logistic计算得到的概率尽量接近 0（即预测目标是bit=1）；在第二层，希望其bit是1，即概率尽量接近1……这么一直下去，我们把一路上计算得到的概率相乘，即得到目标词Wn在当前网络下的概率(P(Wn))，那么对于当前这个sample的残差就是1-P(Wn)。于是就可以SGD优化各种权值了。

从根节点开始，对于一个sample而言，目标词是W2，二进制编码是"110"。我们在根节点计算得到它的第一位是'1'的概率是P，那么它第一位是 '0'的概率就是1-P；在左子树里，第二位是"1"的概率是P'，那么第二位是"0"的概率就是1-P'，而在右子树里，第二位是"1"的概率是 P''，那么第二位是"0"的概率就是1-P''；第三位亦如此。为方便表示记，我们只写到第二层。这样，在第二层，整个概率之和就是

(P*(P') + P*(1-P')) + ((1-P)*(P'') + (1-P)*(1-P'')) = P + (1-P) = 1

即按照目标词的二进制编码计算到最后的概率值就是归一化的，这也是为啥它被称作hierarchical softmax的原因。

word2vec功能

功能具体如何实现有待后续添加

1）计算两个词语相似度。

2）列出所有相似词语列表。

3）寻找对应关系：男人-男孩女人-？内蒙-呼和浩特河北-？

4) 删选不合群的词语，可以用来做特征选择

5）测试词向量的加减

http://blog.sina.com.cn/s/blog_584a006e0101rjlm.html

http://blog.csdn.net/zhoubl668/article/details/24319529