
朴素贝叶斯分类是一种十分简单的分类算法,朴素贝叶斯根据给定的特征向量(若干个特征写成一行),求解在所以特征值都出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。用公式表示为
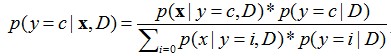 y=c表示类别为c,粗体x表示一个特征向量,D是指当前数据集,因为学习是在某数据集的条件下。
y=c表示类别为c,粗体x表示一个特征向量,D是指当前数据集,因为学习是在某数据集的条件下。
可以看出,求某个类别在某些条件下出现的概率,使用的是贝叶斯公式,第一章已经提到。并且,公式的分母其实都一样,所以公式的左端正比于公式的右端分子,即每次只计算分子,哪个类别的分子大,就预测为哪个类别。从分子我们可以看出,大体上需要计算两个东西,一个是在某个类别时特征向量X出现的概率,一个是每个类别出现的概率。特征向量X意味着多个条件同时满足的概率,这里我们假设每个特征之间是条件独立的,那么就有![]() 即每一维特征出现的概率相乘,因为他们是独立的,和事件的概率等于各个事件独自出现的概率相乘。
即每一维特征出现的概率相乘,因为他们是独立的,和事件的概率等于各个事件独自出现的概率相乘。
接下来要做的就是去估计上面这些概率值。包括p(xi|y=c,D),p(y=c|D)。直观的想法是用频率当作概率,p(xi|y=c,D)=数据中所有类别为c的子集中,xi特征出现的频率,p(y=c|D)=所有数据中c类出现的频率。严谨的证明需要用MLE(极大似然估计)求解,得到的答案恰好如上所述。代码就更好写了,循环做统计就可以。
MLE推导过程如下:
单个数据点出现的概率:
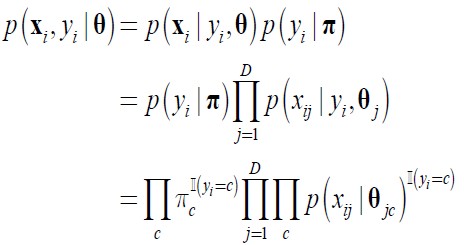
其中D是一条数据的特征维数,c是类别是数目。公式第一步采用链式规则,第二步我们提到过,各个特征条件独立,所以概率直接相乘。第三步多出了两个连乘符号是为了统一所有数据点的公式格式,其中I(yi=c)的含义是当yi=c是取值为1否则为0。虽然它是个连乘,但是其实只有一个值起作用,即数据点所属的那个类别的概率。我们假设类别服从分类分布,特征只取0,1二值,服从01分布。
所有数据点乘在一起的对数似然函数为:
![JB{`2JXL(`K0W]0}]AU_SL8.jpg](/uploadimage/551597505608028160.jpg)
然后求解argmax l(θ) s.t.![]() 利用拉格朗日乘子法,得
利用拉格朗日乘子法,得![]()
分别对其中的pi和θ求偏导=0,求得参数。
最后解为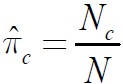
![9F]6EZZHVWN%VZDA7}13SBR.jpg](/uploadimage/551606261255376896.jpg)
下面看一个例题
假设一个数据集,有三维特征,每个特征只取两个值0或1,类别标签也只取0,1,数据如下
A | B | C | y |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 0 |
1 | 1 | 0 | 0 |
0 | 0 | 1 | 1 |
1 | 1 | 1 | 1 |
1 | 0 | 0 | 1 |
1 | 1 | 0 | 1 |
那么对一个新的输入A=0, B=0, C=1,朴素贝叶斯分类器将会怎样预测y。
首先分别计算概率:
p(A=0|y=0)=2/3 p(B=0|y=0)=1/3 p(C=0|y=0)=2/3
p(A=0|y=1)=1/4 p(B=0|y=1)=1/2 p(C=0|y=1)=1/2
预测:
p(y=0|(0,0,1))正比于p(A=0|y=0)*p(B=0|y=0)*p(C=1|y=0)*p(y=0)=2/3*1/3*(1-2/3)=2/27
p(y=1|(0,0,1))正比于p(A=0|y=1)*p(B=0|y=1)*p(C=1|y=1)*p(y=1)=1/4*1/2*(1-1/2)=1/16
p(y=0|(0,0,1))最大,预测y=0.
由于数据总是有限的有时统计的概率总会出现0概率,即某个特征的某个取值在某个类别下从未出现过,在训练数据中未出现过并不意味这实际中不会出现。并且只有计算值出现一个0,由于是相乘关系,那么得到的最终概率一定是0,这会对预测结果的准确性有很大的影响。这里我们使用拉普拉斯校准避免0概率出现,它的基本思路是匀出一点点概率给那些没有出现过的特征值。做法如下,如果有0概率,那么这个特征下每一个取值出现的次数都加一次。例如,假设在y=1时,A=1出现4次,A=0出现0次,那么每个值都加1,即A=1出现5次,A=0出现1次,注意此时中次数变为6次而不是次。p(A=1)=(4+1)/(4+2), p(A=0)=(0+1)/(4+2).
贝叶斯估计与极大似然估计的不同在于贝叶斯估计加入了先验知识。贝叶斯估计认为所求的参数是符合某一分布的随机变量,这一分布由先验知识决定,为了方便计算一般采用共轭先验。共轭先验的特点是当参数不再是一个特定变量而是一个分布时,这个先验分布和后验分布的式子乘在一起很容易化简。另外极大似然估计可以看作参数是服从均匀分布的贝叶斯估计。
举个例子,第一章的极大似然估计例题采用的投硬币的例子,得到的参数估计是4/5,假设这是有个赌徒,他很擅长投硬币,他掂一掂硬币就知道这硬币朝上概率大约在哪个范围浮动,这时他说,这个硬币比较均匀,朝上概率应该是4/7,那么你是否该怀疑自己的估计值。有了这些知识,所求参数就不再是均匀分布,而应该更倾向于某个范围,把这个分布函数加入你的估计方程中,就是贝叶斯估计。
这里给出采用贝叶斯估计求得的二值特征的二分朴素类贝叶斯的参数估计公式:
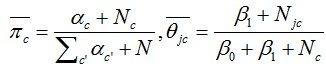
其中α和β是先验参数,这些参数调节了数据对最终参数的影响,α和β较大的话,先验知识会起较大作用。
前面的推导都是用的离散值特征,特征的取值可以枚举,那么可以方便的统计出每个值出现的频率,当作他们的概率。当数据是连续值时,该如何处理。我们知道正态分布在实际中非常常见,由中心极限定理可知,特征值服从均值为u,方差为σ的正态分布。均值和方差可以由数据的平均值和方差估计。有了这两个量,我们就可以通过正态分布的公式算出任何一个值的概率。
总结一下有哪些改动,1.训练阶段计算出每个特征在每个类别下的均值和方差。2.预测阶段的概率不是直接相除得到,而是利用均值方差和正态函数求出的。
PS:这里谈一点经验,通过做的几个实验发现,当处理连续值时,对特征的取值范围适当的缩放会对准确度有不小的影响。这个以后会提到。