
一个学期结束了,期末匆匆忙忙的开发了这个博客系统,当时壮志雄雄的说,等我博客上线了,我一定要把这学期学的东西整理成博客,第一个文集就叫机器学习。25号考完了机器学习就赖在床上一整周,甚至博客系统有些东西都没开发完,囧。直到前天才强打精神,算是大体上把博客开发完成了,虽然有些边边角角还是需要继续修的,不过发了几篇博客感觉还是不错的,赞一个。
前天昨天今天把以前一些个小玩意稍稍整理了一下发了几篇博客,语言都不完全,完全是先占个坑。以后慢慢的补,一方面是为了测试博客,一方面是先列个大纲。
这个文集不仅是机器学习这一门课程的内容整理,还参考了相关的其他几门课程,都整合在了一起,其中也有一些知识是网络上的内容,会标记出转载出处。文集中内容不会太深入,数学证明也不会一列一大堆,一方面列一大堆也没人看,另一方面编辑公式好麻烦。。。文章的内容尽可能的直观易懂。对机器学习有一个感性的认识,掌握一些经典算法的基本用法是这个文集的主要目的。督促自己学以致用,温故知新是这个文集的初衷。所以这个文集适合于刚刚接触机器学习,想要了解机器学习的人。有了这些认识,对深入的看数学证明有很大的帮助。
先上机器学习知识点笔记第一章,这一章是我整理的一些我在学学习机器学习过程中经常用到的一些数学知识。先把这些知识复习一下,对于以后看那一大堆的推导具有很大的帮助。
它 将对一复杂事件A的概率求解问题转化为了在不同情况下发生的简单事件的概率的求和问题。如果事件B1、B2、B3…Bn 构成一个完备事件组,即它们两两互不相容,其和为全集;并且P(Bi)大于0,则对任一事件A有 P(A)=P(A|B1)*P(B1) + P(A|B2)*P(B2) + ... + P(A|Bn)*P(Bn).
贝叶斯公式用来描述两个条件概率之间的关系,比如 P(A|B) 和 P(B|A)。按照乘法法则:P(A∩B)=P(A)*P(B|A)=P(B)*P(A|B),可以立刻导出。如上公式也可变形为:P(B|A)=P(A|B)*P(B)/P(A)。而其中的P(A)可以由全概率公式展开。得到最终的贝叶斯公式
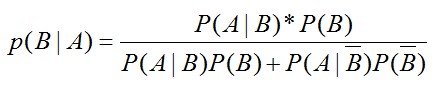
如果B事件是有多个独立子事件构成,那么公式如下:
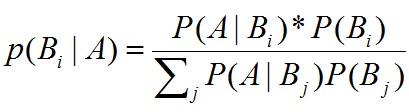
(1)Bernoulli分布
又名两点分布或者0-1分布。若Bernoulli试验成功,则Bernoulli随机变量X取值为1,否则X为0。记试验成功概率为θ,即P(X=1)=θ,p(X=0)=1-θ。均值μ=θ,方差 =θ(1-θ)
(2)二项分布
二项分布即重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为n重伯努利实验
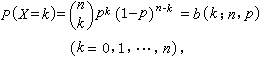
(3)多项分布
把二项分布公式推广至多种状态,就得到了多项分布。例如1出现k1次,2出现k2次,3出现k3次的概率分布情况。
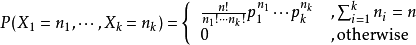
(4) 泊松分布
这个分布是S.-D.泊松研究二项分布的渐近公式时提出来的。泊松分布P (λ)中只有一个参数λ ,它既是泊松分布的均值,也是泊松分布的方差。在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布。
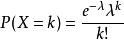
(1)均匀分布
随机变量X在区间[a,b]上均匀分布。
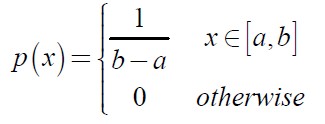
(2)高斯分布
对模型残差或噪声能很好建模。
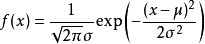
(3)t分布,laplace分布,gamma分布,beta分布
Laplace分布:相比于高斯分布,Laplace分布更集中有均值附近。均值=u,方程=2b2
![KYIH]D~A)NPLI){_PT4O5J1.jpg](/uploadimage/550922665859354624.jpg)
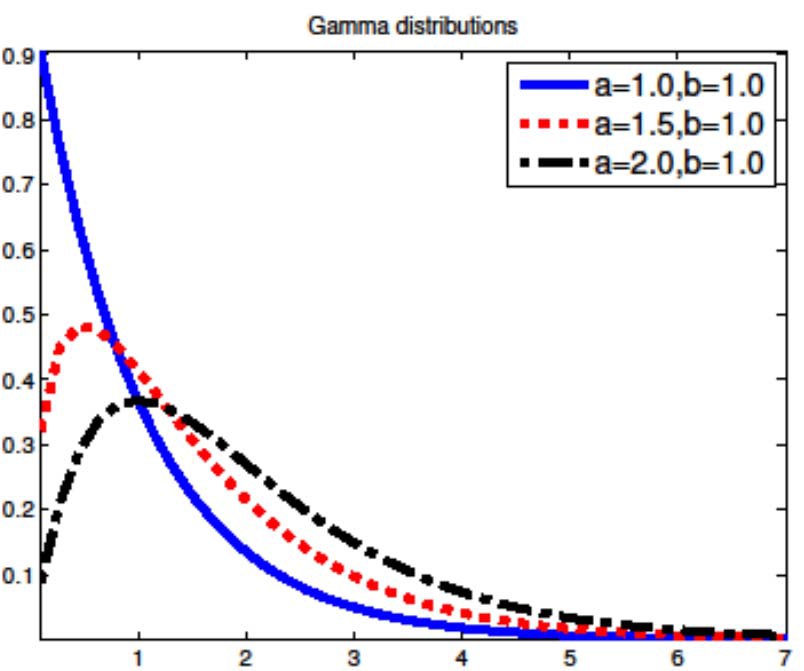
Gamma分布:a为形状参数,b为比率度参数
![9O@%SB(S]}@AU{)659]VC35.jpg](/uploadimage/550923588102918144.jpg)
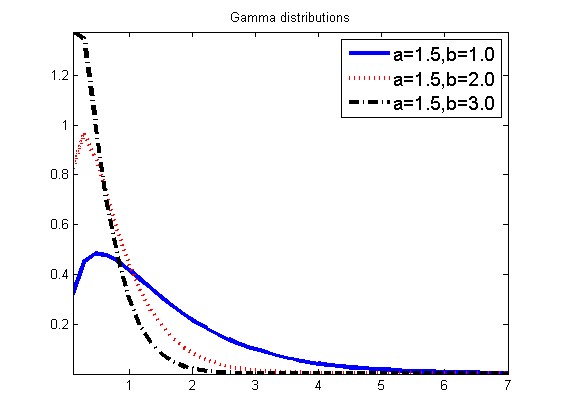
Beta分布:beta分布的支持区间为[0,1]
当0<a<1,0<b<1时,在0,1处有两个峰值。
当a>1,b.1时有单个峰值
a=b=1时,为均匀分布
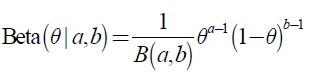
![0RZ)UQ]K`08BZ$NVCN(@$U2.jpg](/uploadimage/550925327866662912.jpg)
独立同分布的随机变量序列X1,x2,...,Xn,E(Xi)=u,方差σ2,则样本均值依概率收敛于期望u。即
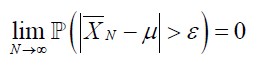
中心极限定理:设从均值为μ、方差为σ^2;(有限)的任意一个总体中抽取样本量为n的样本,当n充分大时,样本均值的抽样分布近似服从均值为μ、方差为σ^2/n 的正态分布。
极大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆就把这个参数作为估计的真实值。
求极大似然函数估计值的一般步骤:
(1) 写出似然函数,即每个随机实验出现概率相乘,为这个抽样出现的概率。
(2) 对似然函数取对数,为了方便求导;
(3) 对参数求导数。
(4) 令导数=0,即求解极值,由实际情况知,该极值为极大值。解似然方程。
例:
一个不均匀的硬币,随机扔了5次,每次记过记为Xi,分别为 正,负,正,正,正。求正面朝上概率θ的极大似然估计.
似然函数:![]() 。
。
取对数,logL(θ)=4log(θ)+log(1-θ)。
对logL(θ)求导![]() 。
。
导数=0,解出θ=4/5,与直观相符。当极大死让估计用于推导贝叶斯分类器公式时,虽然过程复杂了一些,但是结果就像这个例题一样,与直观符合,结果非常的简单。
--概率论部分引用自国科大卿来云老师课件
(1) 矩阵Y对标量x求导:
相当于每个元素求导数后转置一下,注意M×N矩阵求导后变成N×M了
Y = [y(ij)] --> dY/dx = [dy(ji)/dx]
(2)标量y对列向量X求导:
注意与上面不同,这次括号内是求偏导,不转置,对N×1向量求导后还是N×1向量
y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)'
(3)行向量Y'对列向量X求导:
注意1×M向量对N×1向量求导后是N×M矩阵。
将Y的每一列对X求偏导,将各列构成一个矩阵。
重要结论:
dX'/dX = I
d(AX)'/dX = A'
(4)列向量Y对行向量X’求导:
转化为行向量Y’对列向量X的导数,然后转置。
注意M×1向量对1×N向量求导结果为M×N矩阵。
dY/dX' = (dY'/dX)'
(5)向量积对列向量X求导运算法则:
注意与标量求导有点不同。
d(UV')/dX = (dU/dX)V' + U(dV'/dX)
d(U'V)/dX = (dU'/dX)V + (dV'/dX)U'
重要结论:
d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = A
d(AX)/dX' = (d(X'A')/dX)' = (A')' = A
d(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X
(6)矩阵Y对列向量X求导:
将Y对X的每一个分量求偏导,构成一个超向量。
注意该向量的每一个元素都是一个矩阵。
(7)矩阵积对列向量求导法则:
d(uV)/dX = (du/dX)V + u(dV/dX)
d(UV)/dX = (dU/dX)V + U(dV/dX)
重要结论:
d(X'A)/dX = (dX'/dX)A + X'(dA/dX) = IA + X'0 = A
(8)标量y对矩阵X的导数:
类似标量y对列向量X的导数,
把y对每个X的元素求偏导,不用转置。
dy/dX = [ Dy/Dx(ij) ]
重要结论:
y = U'XV = ΣΣu(i)x(ij)v(j) 于是 dy/dX = [u(i)v(j)] = UV'
y = U'X'XU 则 dy/dX = 2XUU'
y = (XU-V)'(XU-V) 则 dy/dX = d(U'X'XU - 2V'XU + V'V)/dX = 2XUU' - 2VU' + 0 = 2(XU-V)U'
(9)矩阵Y对矩阵X的导数:
将Y的每个元素对X求导,
--转自http://lzh21cen.blog.163.com/blog/static/145880136201051113615571/
(1)trace(AB)=trace(BA),trace(ABC)=trace(CAB)=trace(BCA)
(2)d(trace(AB))/dA=B'
(3)trace(A)=trace(A')
(4)trace(a)=a,a为实数
(5)d(trace(ABA'C))/dA=CAB+C'AB'