
产生式分类器:对联合分布p(x,y)建模
– 产生:能从联合分布p(x,y)中产生数据
– (朴素)贝叶斯分类器
– LDA/QDA
判别式分类器:直接对p(y|x)建模
– Logistic回归
– 感知机/神经元网络
– SVM
logistic回归是对线性回归的扩展,它在线性回归的结果上再利用sigmod函数进行了一次映射。用函数表示成![]() 。
。
其中WT *X是前面提到的线性回归的表达式,sigm是sigmod函数,形式为![]() 。sigmod函数是一个S形函数,它将线性回归的结结果映射到(0,1)区间。
。sigmod函数是一个S形函数,它将线性回归的结结果映射到(0,1)区间。
这里我们只讨论类别是二值的分类。所以目标变量y服从伯努利分布。综合起来为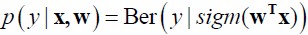 。
。
![OH}A)V`{G~5A{SJPX5]TYUU.jpg](/uploadimage/554552413386838016.jpg)
前面提到,目标变量y服从伯努利分布,并且给出了分布函数,下面就是通过MLE估计一个最优的W,使得该数据出现的概率最大。如果从统计决策理论看,我们可以将MLE看作是采用负log似然损失(negative log likelihood, NLL),使损失最小。
![UUS4AD]2ADL{UJ4B~7LZ]W8.jpg](/uploadimage/554556216152559616.jpg)
我们要是的J(w)最小,采用和前面提到的线性回归相同的算法,只是梯度公式变化。