线性回归介绍

    线性回归是利用数理统计中的回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。我们假设有n维特征，用公式表示为y=f(X)+ε.其中X是一个n+1维的向量，用点积形式表示为，w和x都是n+1维向量，其中n维是特征，最后1维是一个常数，或者叫截距项。我们要计算的就是这个w向量，w成为权重向量，有了w，根据公式就可以计算出y。

    上图给出了一个房价预测的例子。房价预测就是用前面的四列特征，计算出房子大体的价格。也就是我们要求一个公式price=a*x1+b*x2+c*x3+d*x4+e的一个公式，使这个公式在训练集上误差最小。求得一个w向量(a,b,c,d,e)在数学中我们已经学过了最小二乘法，他使得平方误差和最小，有公式，X是特征矩阵，y是类别向量。

    有了上述公式其实我们并不直接按公式计算，而是采用QR分解或者SVD分解来进行计算。推导过程在矩阵分析相关书籍中有详细介绍。另外需要说明的是，在机器学习中通常是提出一个模型，然后选择一个损失函数，然后问题成为一个最优化问题，求一系列参数，使得损失最小。在最小二乘法中，使用的平方误差，可以看作是L2损失，即平方损失函数。

MLE

预测的y是连续值，我们假设它服从正态分布，也就是说在真实值附近概率大些。

极大似然函数为，极大似然可等价地写成极小负log似然损失（negative log likelihood， NLL）。将整体分布的概率模型带入，得到

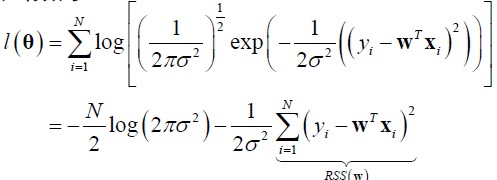
    前面是常数，我们只优化后半部分，其中RSS表示残差平方和(residual sum of squares)，可以看到优化的公式和最小二乘法一样。如果将NLL写成矩阵乘的形式，然后只取与W有关部分，求导=0，就可以解出最小二乘法的公式。

梯度下降法

    梯度下降法是利用高数中梯度概念，设计的一个逐渐逼近算法。

    首先说一下梯度。在向量微积分中，标量场的梯度是一个向量场。标量场中某一点上的梯度指向标量场增长最快的方向，梯度的长度是这个最大的变化率。由于我们这里是让一个损失函数最小，那么梯度方向就是一个梯度损失降低最快的方向，我们每次都将W向这个方向上挪动一点点，逐渐的就会挪动到极小值。梯度向量求法也很简单，即函数对每一个变量求偏导。

在这里，我们要求解w，即求解，使得L2损失最小。粗体Xi是一条数据，N是数据的总数。f(xi)-yi就是预测值与真实值之间的误差。梯度下降的公式如下：

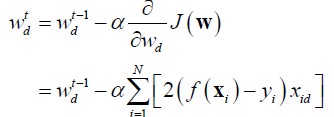
对J(W)求偏导即是梯度，通过不断的迭代w，得到极小值的一个近似解。alpha是学习率，控制了挪动的步伐大小。当每次的变化很小的时候就可停止程序。下图显示了线性回归一条直线的路径，昨天是梯度的等高线，中间低两段高，蓝色的线就是梯度的方向，通过一点点的沿梯度方向挪动，最后下降到极小值附近。

随机梯度下降

在上述算法中，我们每次利用了所有的数据，效率比较低，我们也称它为批处理梯度下降算法。为了提高效率，随机梯度下降每次只使用一条数据。

他有如下优点：

1. 收敛速度通常较快

2. 不太容易陷入局部极值

3. 对大数据尤其有效

4. 可以在线学习