
1943年McCulloch和Pitts发表文章,提出M-P模型。描述了一个简单的人工神经元模型的活动是服从二值(兴奋和抑制)变化的。总结了神经元的基本生理特性,提出了神经元的数学描述和网络的结构方法。——标志神经计算时代的开始
![]L{_IY0BKG7AN0028}%$T3M.jpg](/uploadimage/554910086896685056.jpg)
神经元的输入有两种类型:兴奋边/抑制边;
神经元的输出有两种状态, 兴奋/抑制;
如果一条抑制边处于激活状态, 则神经元处于抑制状态;
如果没有抑制边处于激活状态, 则当兴奋边的数目超过一个阈值时, 神经元处于兴奋状态, 否则处于抑制状态;
特点
边的权值都为固定值1, 无法调整;
阈值;
输出是0/1;
一票否决;
改进
统一兴奋边和抑制边
边的权值都为固定值1 -> 权值可调整
一票否决-> 相对抑制
改进后的神经元模型
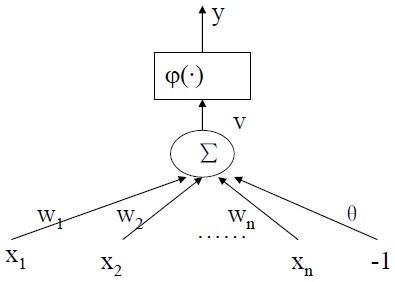
其中v是一个线性函数![){L]ZA%Y{C]YIJ)]WW%~$S4.jpg](/uploadimage/554911453988130816.jpg) ,跟线性回归是一个样子。其中的φ()函数是一个活化函数,有线性活化函数,分段活化函数,阈值活化函数,和sigmod活化函数。如果φ采用了sigmod函数,那么只一个神经元其实就是表示的是一个logistic回归。
,跟线性回归是一个样子。其中的φ()函数是一个活化函数,有线性活化函数,分段活化函数,阈值活化函数,和sigmod活化函数。如果φ采用了sigmod函数,那么只一个神经元其实就是表示的是一个logistic回归。
1957年Frank Rosenblatt定义了一个神经网络结构,称为感知机(感知器,Perceptron)。感知机主要的本质缺陷是它不能处理线性不可分问题。
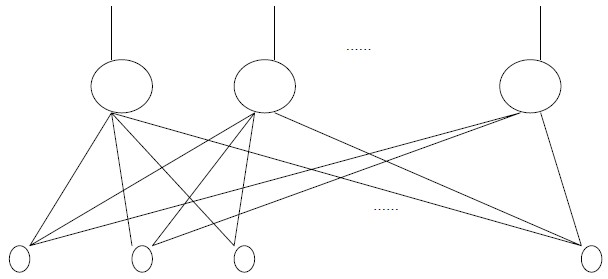
略过
![04]U%4%[PJE3B2E13YO@6]S.jpg](/uploadimage/556709007495139328.jpg)
将网络中的所有参数初始化化一个小随机数。
给定隐藏层或输出层的单元j,到单元j的净输入Ij 表示为![]() 。是前一层输出的一个线性组合。其中隐藏层的净输入公式中的字母O代表的是输入层输入的特征值。隐藏层和输出层对净输入使用激活函数,一般为logistic函数,公式为
。是前一层输出的一个线性组合。其中隐藏层的净输入公式中的字母O代表的是输入层输入的特征值。隐藏层和输出层对净输入使用激活函数,一般为logistic函数,公式为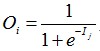 。
。
对于输出层单元j的误差计算公式为Errj=Oj(1-Oj)(Tj-Oj)。注意Oj(1-Oj)是logistic函数的导数。
对于以藏层单元j的误差计算公式为Errj=Oj(1-Oj)sum(Errk * wjk)。wjk是到下一层单元的连接权重。
计算完误差之后,根据误差更新权重和偏倚。w的改变值Δwij=(l)ErrjOi wij=wij+Δwij l是学习率。偏倚有下式更新Δθj=(l)Errj θj=θj+Δθj
BP模型训练过程其实就是梯度下降的过程,前一层的误差可以由后一层的误差表示出。
对只有一个隐层的网络,在隐层中使用sigmoid函数,则上述过程可以以任意精度逼近任何平方可积函数。
采用梯度法,可能陷入局部极小;迭代算法,收敛速度慢; 隐层节点数目的确定没有理论指导,只能根据经验选择。